Расчет устойчивости для произвольных по сложности конструкций
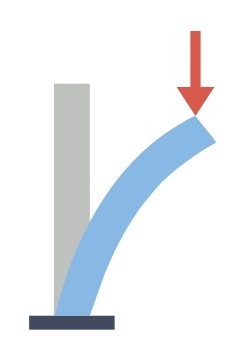Устойчивость в механике
Если в механической конструкции имеются протяженные элементы, то обеспечения только их статической прочности недостаточно. Разрушение конструктивного элемента при увеличении его длины может произойти не вследствие потери прочности, а из-за потери устойчивости. По этой причине в расчет статической прочности протяженных деталей необходимо включать проверку устойчивости.
Под устойчивостью понимается свойство системы сохранять свое состояние при внешних воздействиях. Понятие устойчивости играет очень важную роль в механике. Дело в том, что если какая-либо механическая система сконструирована без учета требований устойчивости, то она будет чувствительна даже к незначительным внешним воздействиям, а это в конечном итоге может привести к самым нежелательным последствиям. Переход системы в неустойчивое состояние, или потеря устойчивости, так же опасен, как и потеря ее прочности, т. е. способен вызвать полное разрушение конструкции. Именно поэтому крайне важно определить границы перехода механической системы от устойчивого состояния к неустойчивому.
Под устойчивым понимается такое состояние механической системы, находясь в котором, она при приложении любого сколь угодно малого внешнего воздействия (т. е. воздействия, которое является не только малым, но может быть сделано меньше любой наперед заданной величины) возвращается в исходное положение равновесия после снятия внешних силовых факторов. Значение внешней силы, при которой система переходит из устойчивого состояния в неустойчивое, называется критической силой. Доля внешней нагрузки по отношению к критической называется запасом устойчивости.
Прямой центрально сжатый стержень при малых усилиях сжатия восстанавливает первоначальное положение и остается прямолинейным после снятия нагрузки. Возрастание осевой нагрузки может привести к резкому увеличению деформаций изгиба. При больших значениях деформаций изгиба могут появиться признаки пластического деформирования, вследствие которых стержень не вернется в исходное состояние, а его ось останется криволинейной. Если возникает такое явление, то говорят, что стержень потерял устойчивость. Следует отметить, что пластические деформации могут быть вызваны и деформациями растяжения, но в этом случае изогнутая ось стержня остается прямой. Отсутствие пластических деформаций при растяжении можно проверить по условию прочности, а при сжатии – по условию устойчивости.
Увеличение линейных размеров конструкции при постоянстве внешних силовых факторов также может привести к возникновению сильных пластических деформаций и даже к ее разрушению, несмотря на то, что все условия статической прочности будут выполнены.
Подобных примеров можно привести множество. Все они указывают на исключительную важность понятия устойчивости в механике.
Основы проведения расчета
В программных продуктах линейки APM имеются инструменты, которые выполняют процедуру анализа по критерию устойчивости. Для выполнения этих процедур используется метод конечных элементов (FEM), реализованный для стержневых, пластинчатых, оболочечных, твердотельных моделей и их комбинаций. Результат расчета устойчивости зависит от геометрии расчетного объекта и от условий его нагружения и закрепления. Различают общую потерю устойчивости и потерю устойчивости в локальных зонах (потерю местной устойчивости). Анализ областей потери устойчивости можно выполнить визуализацией форм потери устойчивости.
Расчет устойчивости проводится одновременно со статическим, поскольку для анализа устойчивости необходимо знать напряженно-деформированное состояние объекта исследования в статике. Расчет устойчивости (по Эйлеру), также как и статический, ведется по недеформированной схеме конструкции. Математически задача устойчивости формулируется как задача на собственные значения, результатом выполненного анализа является коэффициент запаса устойчивости и визуальное представление форм потери устойчивости.
