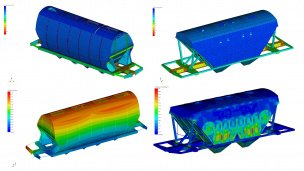
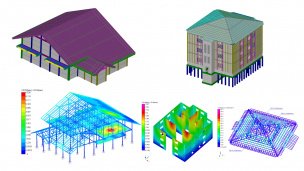
Анализ напряженно-деформированного состояния конструкций
 Статические (линейные) решения
Статические (линейные) решения
Воздействие силовых факторов на закрепленное материальное тело вызывает его деформацию и, как результат, возникновение напряжений в каждой его точке.
Совокупность напряжений и деформаций, возникающих при действии на твердое деформируемое тело внешних нагрузок, температурных полей и других факторов, называется напряженно-деформированным состоянием (НДС).
При математическом описании НДС деформируемое тело рассматривается как однородная сплошная изотропная среда, механические характеристики которой во всех направлениях одинаковы, при этом в каждой ее точке выполняется условие сплошности. Наиболее эффективным методом анализа НДС является численный метод конечных элементов (FEM), математическая реализация которого заключается в решении систем дифференциальных уравнений в частных производных или интегральных уравнений, описывающих взаимосвязь механических, тепловых, газо- и гидродинамических, электродинамических и других параметров твердого деформируемого тела.
Метод конечных элементов основан на представлении области, в которой ищется решение системы дифференциальных уравнений, в виде конечного количества подобластей, или конечных элементов, вершины которых называются узлами или узловыми точками. Система дифференциальных уравнений в частных производных специальным образом заменяется системой линейных алгебраических уравнений (СЛАУ), количество которых равно количеству неизвестных значений в узлах, на которых ищется решение исходной системы. Это количество, называемое размерностью задачи, прямо пропорционально количеству конечных элементов и количеству степеней свободы каждого из них (стержневые и пластинчатые элементы имеют по шесть степеней свободы, а твердотельные – три) и ограничивается только возможностями ЭВМ.
Проведение статического анализа в продуктах АПМ
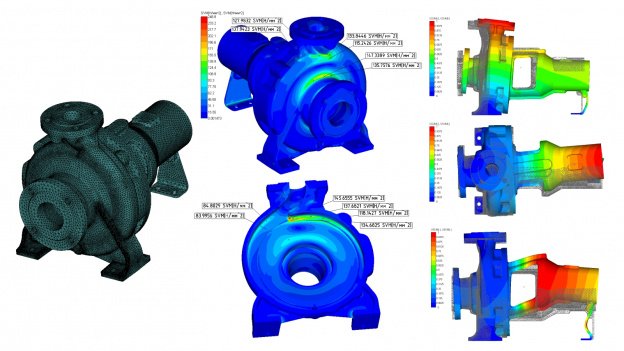
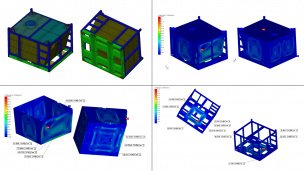
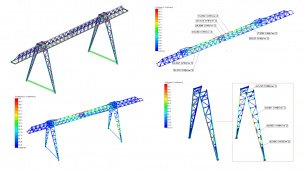
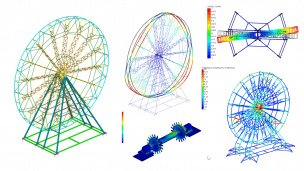
В программных продуктах АПМ реализация метода FEM сводится к анализу перемещений узловых точек. В основе математической формулировки метода лежит вариационный принцип Лагранжа, т. е. принцип минимума потенциальной энергии системы. Неизвестными здесь являются перемещения узловых точек, а напряжения определяются путем численного дифференцирования перемещений. Результатом расчета НДС являются компоненты перемещения узловых точек по трем координатным осям и углы поворота относительно этих осей, компоненты нормальных и касательных напряжений и главные напряжения.
Действующие на механическую систему нагрузки задаются в форме силовых факторов (сосредоточенных и распределенных сил и моментов), кинематических перемещений и температурных полей. Тепловое воздействие, приводящее к появлению термонапряжений и термодеформаций, может анализироваться как отдельно, так и в совокупности с механическим воздействием.
При анализе статической прочности сложное напряженное состояние произвольного объемного элемента сводится к одноосному эквивалентному растяжению. В программных продуктах линейки АПМ используются следующие методы приведения: по Мизесу, Мору, Друкеру – Прагеру, по наибольшим касательным напряжениям, наибольшим главным напряжениям, наибольшим деформациям и т.п.
Обычно величины статических напряжений ограничены пределом прочности или пределом текучести, что позволяет определить коэффициенты запаса статической прочности и текучести.
Статический расчет выполняется как для рассматриваемого объекта в целом, так и для каждой точки его произвольного поперечного сечения. Результаты расчета представляются в виде различного рода полей, эпюр, изолиний, изоповерхностей и т.д.